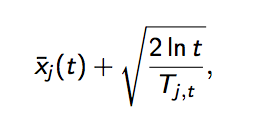从DP到RL
1.对RL的直观感受
首先,RL与其他ML任务不同在哪里?
- There is no supervisor, only a reward signal
- Feedback is delayed, not instantaneous
- Time really matters (sequential, non i.i.d data)
- Agent's actions affect the subsequent data it receives
这里面可能最重要的就是第一条,奖励信号是增强学习的基础,奖励信号需要反映出t时刻agent(robot)在做的事儿到底是好是坏?这是一个scalar。这与普通的监督学习最大的差异是,我没有告诉你此时你应该做什么,我只评价你做的怎么样。
而agent的目标就是使长期的reward最大化。
那么,实际中的例子呢,我们比较熟悉的当然就是deepmind拿它来玩儿各种游戏,以及alpha go了。
因为棋局的输赢以及游戏中的score是比较明确的reward,所以单纯对于RL来说这些任务是比较容易解决的。
另外,如果我们熟悉DP,那么我们来对比一下Planning与RL之间的差异性。
Reinforcement Learning:
The environment is initially unknown
The agent interacts with the environment
The agent improves its policy
Planning:
A model of the environment is known
The agent performs computations with its model (without any
external interaction)
The agent improves its policy
可以看到,规划实际上是RL的某种特例,是在周遭环境可以明确建模情况下的一种自闭型决策过程。因为周遭环境可以建模,规则明确,所以不需要agent对环境发生的反馈与环境对它的反馈是确定性的,并不需要去探索,只在agent内部去进行规划就可以解决问题。而RL实际上可以解决周遭环境开始时无法一下建模,通过逐步与环境交互来进行探索的情况。当然如果是可以用规划解决的问题,RL则是杀鸡用牛刀,费力不讨好,但是对于大多数问题,往往无法精准建模,RL就显得尤为重要。
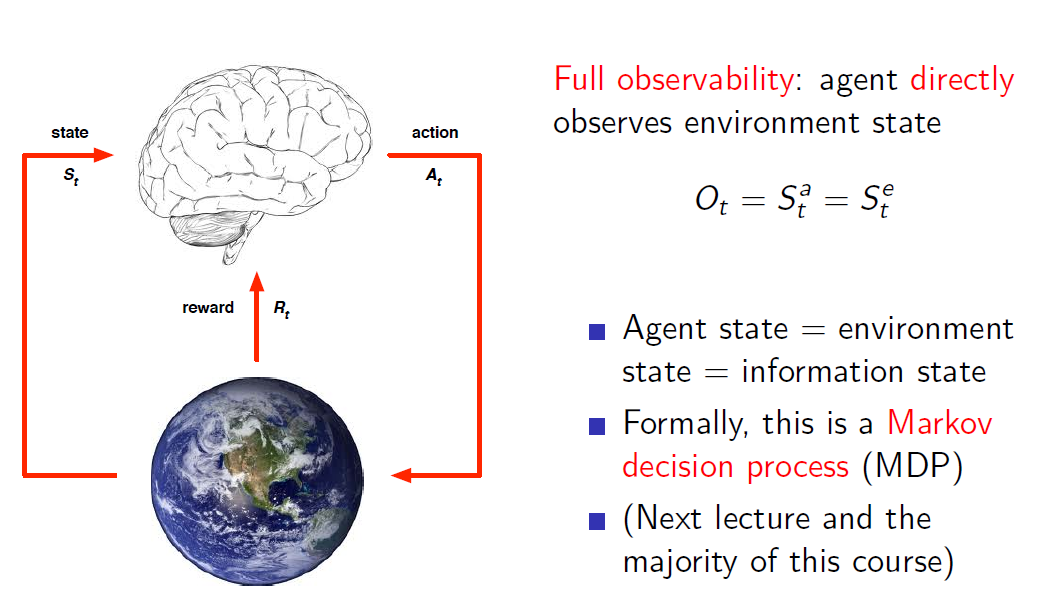
这页PPt的左边图就是一个agent实体与environment交互的过程,agent的每一个action改变env,而env state发生变化,从而agent接受到的信息也发生变化,另一方面环境的变化对agent进行reward反馈,由于agent的目标是使得累计reward最大化,agent就需要考虑这些信息使得来做出下一个action。
而env这个变化如何被agent观察有两种形式,一个是full observe,此时环境状态的变化全部被agent观测到(上帝视角),那么环境状态变化多少则agent状态理应也变化多少。
但往往还存在Partial observability,比如机器人通过看到的周遭并不能得知自己身处何处,打牌只能看到公共牌面(玩家视角)。所以此时env的状态并不能等同于agent的状态。
2.MDP问题
RL中,我们需要构建的就是如果输入观测env,agent如何做出action使得reward最大这样的系统。这其实也算是某种通用人工智能对吧。
好了我们通俗描述的这整个过程,统称为MDP问题,具体描述是:
某个智能体(agent)的初始状态为S0,然后从Action集合A中挑选动作a0做出反应,反应后以概率Ps,a随即转移到下一个状态S1。。。直到终止时刻。我们想要找到的是,终止时刻得到的累计回报最大的策略。
这个和马尔科夫链的区别是,MDP中需要考虑action,也就是需要决策,而马尔可夫仅仅考虑节点之间的转移。
增强学习的本质是学习从环境状态到动作的映射(即行为策略),记为策略π: S→A。我们可以看到一个策略π的长期影响(累计回报)是至关重要的。
那么最重要的在构建RL系统时有三点:
- Policy: agent's behaviour function:
Policy是一种action选择的规则,直观地我们考虑只采用单一policy即----做出使得value function最大的action,这个其实是Exploitation思想,既利用已经得到的知识来决定策略,往往在测试时使用这样的策略。
但是在训练中我们需要加入一些随机性,使得许多情况能够被探索,就是说虽然我认为你最有可能做action A获得最大收益,但还是有可能采用其他action,这样的训练过程所利用的是Exploration思想。
- Value function: how good is each state and/or action:
这就是对future reward的一个预期,一般表示为这种形式:
其中R就是对应时刻的reward值,gamma是一个衰减函数,很显然离当前时刻越近的预期对我的判断影响越大。
Value function其实又细分为action-value function和state-value function.
前者一般用q(s,a)表示,依旧是value function的形式,意义为当前状态下,我们选择一个动作,对此的(最大)价值估计
后者一般表示为V(s),意义为当前状态下的(最大)价值估计,显然有V(s)=max(q(s,a))
这中Value function也叫做Bellman 方程
RL里面我们较常用的是动作价值函数
- Model: agent's representation of the environment:
Model主要建模agent对这个世界的认知,
分为两个部分,一个是对自身state的建模,也就是构建状态转移矩阵。另一个是对每一个sate,每一个action的reward的建模。
3.DP求解
好了,现在我们有了MDP的问题描述,Bellman方程,求解这样的问题,看起来使用DP就可以了啊。确实是的,但有一个我们忽略的重要前提----需要对环境的完整构建。也就是说,我们在求解DP问题时,往往已知了所有q(s,a)的大小。或者说可以通过r(s,a)的大小求得。比如说背包问题,所有物品的价值都是已知的,我们直接去求解
dp( i,j ) = Max( dp( i-1, j ), dp( i-1, j-w[i] ) + v[i] )
这里状态i,j表示可使用前i个物品,剩余背包容量为j时的最大价值估计。i,j的sate(最大)估值由(i-1,j)或者(i-1,j-w[i])的状态估值的较大值得到,action实际上隐含了,分别为选取与不选取,r(s,a)=v[i]or0(选or不选)。这样,我每次获得状态s(i,j)的评估时,只需要访问之前的两个节点dp( i-1, j ), dp( i-1, j-w[i] )就足够了。DP求解的关键是如何设计s(i,j),状态空间和转移规则设计的越精巧,那么评估完整个(i,j)表所需要的次数就越少。
4.MC(Monte Carlo)求解
对于MDP问题里,如果r(s,a)未知的情况下,DP就无法求解。这时候显然我们需要估计r(s,a)。如果领域知识很重要,估计准确时,r(s,a)完全可以合理假设,但也存在难以直接估计的情况。那么我们就需要蒙特卡洛方法。这里为了直观描述蒙特卡洛方法在MDP的应用,举一个例子,但这个例子其实不是一个典型的MDP问题,先上例子:
在我自己的面试经历中,面试官曾经问到这样的一个典型案例,可惜的是我完全知道案例背后的道理,但是从来没有在教材上仔细看过案例的描述,没有将这个案例名称与背后的知识连接起来,没有回答上当时的问题。这个问题其实很出名,广告变形投放,公司管理,投资,医疗试验上都有很好的应用,他就是多臂老虎机问题,描述如下:
多臂老虎机拥有k个手臂,拉动每个手臂所获得的收益遵循一定概率但互不相关,如何找到一个策略,在一定操作次数下使得拉动手臂获得的收益最大化。
这里很显然和value function类似的,我们需要建模在当前次数(t)下,选择哪一个手臂(a),能够获得的期望回报q(t,a)
而,因为我们不知道k臂后的真实分布,我们只有通过尝试,去用均值Q(t,a)=(已经尝试过的a臂收益累加和/已经尝试过a的次数)
逼近期望q(t,a)(当在尝试次数无穷的时候有大数定律保证收敛),但是很显然,我们也不可能无穷次地尝试每一个手臂。
所以有一个trade-off在exploration与exploitation之间。
1.比较简单的解决方案就是所谓epsilon-greedy策略。简言之:大概率选择估值高的action,小概率选择其他action。改变epsilon以增加随机程度。(类似模拟退火)
2.UCB算法,UCB算法全称是Upper Confidence Bound(置信区间上界),不多说了,它的算法步骤如下:
先对每一个臂都试一遍
之后,每次选择以下值最大的那个臂
其中加号前面是这个臂到目前的收益均值,被选中的概率会收到增益,起到了exploit的作用;同时后一项使得被选次数较少的臂也会得到试验机会,起到了explore的作用。
3.Thompson采样
假设每个臂是否产生收益,其背后有一个概率分布,产生收益的概率为p
我们不断地试验,去估计出一个置信度较高的*概率p的概率分布*就能近似解决这个问题了。
怎么能估计概率p的概率分布呢? 答案是假设概率p的概率分布符合beta(wins, lose)分布,它有两个参数: wins, lose。
每个臂都维护一个beta分布的参数。每次试验后,选中一个臂,摇一下,有收益则该臂的wins增加1,否则该臂的lose增加1。
每次选择臂的方式是:用每个臂现有的beta分布产生一个随机数b,选择所有臂产生的随机数中最大的那个臂去摇。
以上就是Thompson采样,用python实现就一行:
choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))
可以看出其本质是假设了每个臂的收益非0即1,也就是伯努利收益,背后是符合beta分布的。
4.Softmax
P(select arm i)=exp(hi/τ)/∑ exp(hj/τ)$$x = y$$
其中,hi是选择i臂的收益均值,τ是类似于模拟退火的常数,比如取值为$$(1/t)$$。如果接近于0,那么将只选择最好的那个,也就是exploitation;反之,如果是趋于无穷(一开始时),将均匀的选取老虎机,也就是exploration。与UCB比较类似,只不过处理均值与探索次数的权衡由加法变成乘法,且输出成分布形式。
类似的多臂赌博机问题是reward分布确定但参数未知的MDP中最简单的问题,因为它的动作只影响reward,而不影响下一个state,所以并不存在planning过程,不属于真正地强化学习范畴。
5.TD(Temporal-Difference)学习
继续看我们的多臂赌博机问题,每一个手臂的均值估计如果我们写成增量表达,有:

其中如果我们考虑上学习率,则有:
$$V(s_t)←V(s_t)+α[R_t−V(s_t)]$$
$$R_t$$是指下一时刻的实际累计回报,比如,多臂赌博机问题有episode=1,所以每次选择结束都可以直接获得累计回报值
但如果对于一个没有明确episode界定的任务,永远不可能知道实际累计回报。
我们想要更新自己的估值函数往往就需要用到TD方法了。把一个episode结束的实际累计回报换成即时回报和下一个时刻的估值
$$Rt=r{t+1}+γV(s_{t+1} )$$
这其实是根据状态价值函数的定义得到的:$$V(s)=E[r(s′|s,a)+γV(s′)]$$
则有:$$V(st)←V(s_t)+α[r{t+1}+γV(s_{t+1})−V(s_t)]$$
这样在episode内就可以实时更新状态节点的估值了,所以TD的方法也就不限于解决episode tasks了。
我们看何时收敛? 当更新不动,也就是当 $$r{t+1}+γV(s{t+1})=V(s_t)$$
TD运用了马尔可夫的一些性质,而MC是广义的随机模拟思想不仅仅局限在MDP中,所以TD在MDP过程表现往往比单纯的MC过程要好(比如收敛速度快)
可能只用文字无法理解,下节我们会给出例子。