Q-learning
Q-learning应该是一种TD的方法,因为本身Q就是马尔科夫过程概率转移矩阵P的时间上的微分,如果对应到离散,应该妥妥的是差分方法,这是因为最终Q矩阵,作为概率转移强度,它应该正相关于获得的最大的收益。所以Q应该也评价策略收益。
但实际上Q-learning更强调的并不是TD的估计方法,而是它是一种Off-Policy,估计的是动作值函数Q(s,a)。
Off-Policy对应的是On-Policy,说的是选择动作时遵循的策略和更新动作值函数时遵循的策略是相同的
让我们通过例子来深刻理解Q-learning的特殊性吧
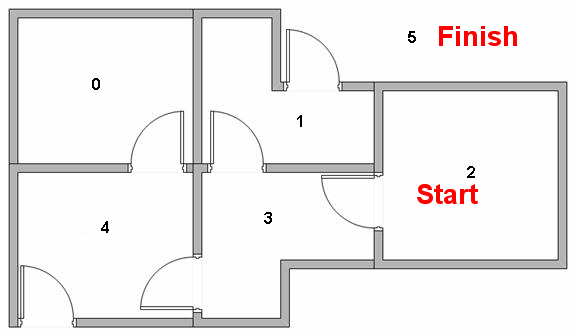
我们用这个例子来加以说明,这个任务是需要从2走到5,房间的连通状态如图所示。那么对于该问题,很简单我们可以将其抽象成数学模型。
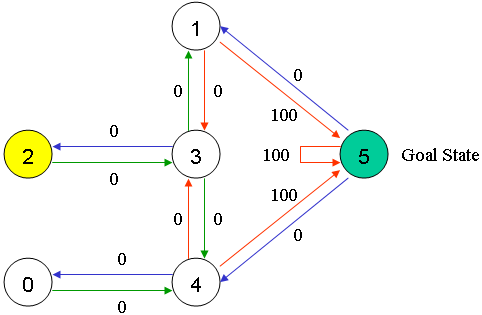
这就是model,其中节点之间的转移规则就是对sate的建模,箭头上的数字代表reward,由于目标是到达5房间,所以它的reward设置成100,这就是对reward的建模。这实际上是一个reward未知的问题,对reward的建模没有对错之分,只有通过实际效果来检验。如果我们写成矩阵的形式:
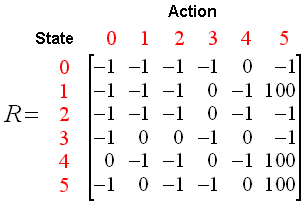
这就是对model的矩阵表达,其中-1指代不可转移。那么我们知道R就可以做出决策了吗?显然是不能的,因为一个sequential decision making需要考虑的一定含有时间这个因子,也就是我在意的不是每个状态能得到的reward,而是我最终(这里是走到5)所得到的reward的累积。
那么value function就是做这种评价的,核心仍然是Bellman方程(这里不是TD的方法),动作估值函数如下:
Q(state, action) =MAX[R(next state,all actions)]= R(state, action) + Gamma *MAX[Q(next state, all actions)]
很显然,把Q(next state, all actions)展开我们就得到value function的形式。注意这里取MAX实际上意味着贝叶斯决策下的价值评估。
--那么系统基本构建完毕,这时候为了解释Q-learning的训练过程我们就从0开始训练一遍,由于训练时我们需要建立的Policy是做exploration的,这里我们采用完全随机。那么,初始化Q(state, action)矩阵为全部0. Gamma=0.8,然后Policy随机(也就是当前状态点到下一状态点按照随机选择),有:

假设我们从2
开始,然后只能转移到3,3可以转移到1,2,4,由于策略是随机的,我们假设随机转移到了1,1可以转移到3或5,假设我们转移到了5.
此时由于Q(1, 5) = R(1, 5) + 0.8 *MAX[Q(5, all actions)]=100,
而由于走到5我们就已经完成了任务,我们称之为完成了一次episode。Q矩阵更新为:

一次训练(episode)既然已经清晰,我们重复前述过程,就可以最终得到收敛的Q,至于如何-判断收敛我们暂且不谈。总之得到收敛的Q:

这时候,由于训练结束。我们通过这样的model,这样的(action)value function,随机的policy得到了我们的Q-learning模型。注意我们之所以说Q-learning是Off-Policy的,指的是,我如何进行选择下一次,与如何更新动作估值用的是毫不相关的两套方案。训练中,更新动作估值使用的是Max{Q(s,a)},与真实的策略(选择哪个a)是没有关系的。
当然在测试时,我们想要看看,是不是模型能够为我走到5号房提供最优策略。这时候我们需要的完全exploitation刚好就是Q-learning动作估值更新的形式---每一个state通过贪婪法来选择下一个state,贪婪的原则就是基于value function(也就是训练得到的Q)
那么我们就得到测试结果:
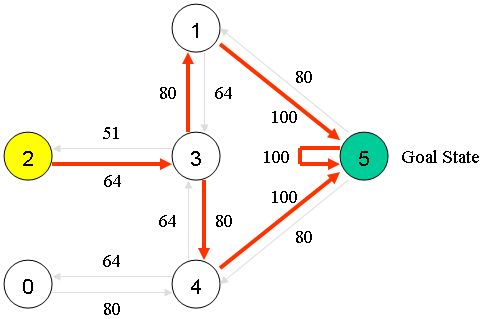
Q-learning属于完全强化学习范畴,是一种value iteration,他通过对Q的学习,最终得到Q也就得到了测试时的最优策略。训练过程中怎样的策略,对收敛性都没有影响,只影响收敛的快慢。而测试时,贪婪的策略又和动作值估计函数中的MAX是同质的(不管采用怎样的训练策略,最终得到的解决方案都只依赖与最终收敛的估值函数),所以Q-learning也称作Value-Based 的。
与之相对的,有policy iteration:
他主要分为两个迭代阶段,首先初始化一个随机策略,第一个迭代阶段是要找到该策略下的价值函数,一般设置阈值在|V-V'|<delta的时候停止迭代,认为已经找到了该策略下的(最大)价值函数(注意,此时仅仅更新价值函数,却在该迭代中一直使用随机策略)
然后开始第二个迭代,既然已经有了这个比较naive策略的价值函数,也就是说我们可以在这样的价值函数下找到一个最优策略(但由于价值函数是naive策略来进行评估的,所以该最优策略并不意味着就是全局最优的策略),那么怎么在一个确定的价值函数下找到最优策略,比如Greedy Policy,每次朝着最优的q(s,a)做决策。
好了做完这个策略更新,之前的价值函数就不适用了,因为我们认为自己的naive策略进步了,我们需要重新对价值函数进行估计。于是返回第一个迭代,从新对我们优化一次后的策略进行评估。整个过程像极了EM算法,收敛性有数学保证,这里就不介绍了。当策略更新不动时,我们就算完成了整个Policy Iteration。
另外训练中结合TD的idea,我们在Q-learning中往往采用的是这个动作值估计函数:
$$ Q(st,a_t)←Q(s_t,a_t)+α[r{t+1}+λmax(Q(s_{t+1},a))−Q(s_t,a_t)]
$$
好了,我们现在了解了Q-learning的过程。可是却发现与神经网络关系不大,那么我们现在准备从Q-learning到Deep Q-learning。