为什么要是高斯分布?

直接粘我逼乎的回答:

因为独立同分布中心极限定理. 其大概意思是:设随机变量相互独立，具有相同的分布,则n个随机变量的和的分布函数(当n趋于无穷)符合高斯分布. 比如galton钉板实验.是比较好理解且直观的例子.

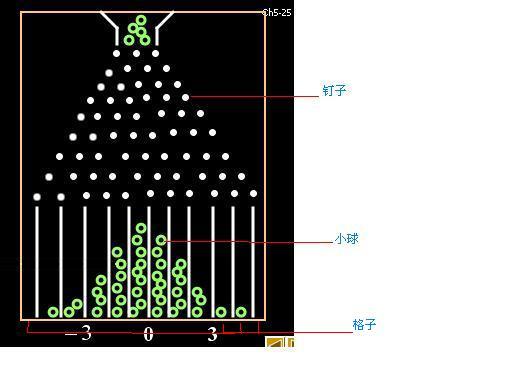
这里的（棣莫弗—拉普拉斯定理） 比较特殊.一次投球过程是一个n重不努力(雾)分布,这里随机变量X指的是小球每次遇到钉板向左还是向右.统计结果指的是经过n次抉择后小球总的向右偏移量(落入的格子).这里符合高斯分布.

这里有很多球只是看作随机模拟,对分布结果的采样,并不表示n个小球是n个随机变量.小球的掉落只是整个统计事件的象征,n个小球只是展示分布结果的一种手段.这里需要n趋于无穷大的是钉板的层数.

没错,不管这n个随机变量自己怎么分布,这里是二项分布,但无论他是均匀分布还是什么奇葩分布,只要他们互相独立且同分布!那么取n个的结果就服从高斯分布!

有人说,钉板换成通道,100%走向一个方向.同样的是高斯分布的特例,只不过sigma为0罢了,全数据为均值.

因为大部分事情在人类不知道其本质的情况下,我们都假设其为独立同分布的.所以其大量统计规律理所当然就是高斯的.如果你接受了这个事实,那么就很好理解为什么高斯这么广泛地应用.

那么就可以直观地理解一下贝叶斯判决,MLE以及QDF和高斯的关系

很简单,我将galton钉板实验的随机变量进行更换(意味着我有两种钉板).由于各自特征的影响导致了其随机变量分布函数的不同.那么根据我们的经验,尽管分布函数不同,它的统计结果(经过钉板)的落点仍然是符合高斯分布.

当然由于分布函数有差异,导致统计结果虽然都是高斯的,但是其均值与方差有不同.可能如下:

那么通过galton钉板实验,就可以看出两种钉板的区别.或者说两类事件的区别.这个时候如果我不知道小球是通过哪个钉板落下来的.你问我,哪个是从A落下的(分类问题)...(假设红色是A分布,蓝色B分布)我会告诉你绿色竖线左边都是A,右边都是B.这个绿色线就是贝叶斯判决面(使用的是MLE思想),因为在绿线左侧,A分布函数大于B的.尽管可能还是有少量B掉到了左边.

高斯与分类的联系

前一个例子比较特殊.再举一个例子,假设班里的男生的四级成绩是高斯分布.这里男生就是一类数据,随机变量就是每一个人的成绩,则每一个男生之间四级成绩是独立且同分布的.假设女生也一样.但是属于不同的分布(导致了均值方差不同).那么只要人数够多(n趋于无穷大),其统计结果就是高斯的.且由于类别的特征导致其分布均值方差不同,可以由MLE作出分界面达到分类.

当然独立同分布的假设虽然很适用,但主要还是看效果来推原因的一件事儿.比如说身高看起来是独立同分布,实则不然.故身高的统计并非高斯分布而是幂律分布.